Определение оптимального размещения логистических мощностей

Определение оптимального размещения логистических мощностей

Доктор технических наук, профессор А.Г. Мадера
Российская Академия наук

В статье показано, что широко распространенный в логистической литературе метод «центра тяжести» не позволяет находить координаты оптимального расположения склада и не обеспечивает минимума целевой функции, выражающей логистические издержки. В статье излагается метод, позволяющий, в отличие от метода «центра тяжести», находить оптимальные координаты размещения склада относительно поставщиков и потребителей, минимизирующие целевую функцию логистических издержек. Приводятся также формулы, оптимальных координат склада, учитывающие влияние на логистические издержки транспортных тарифов и времени доставки грузов от поставщиков на склад и со склада к потребителям.

Введение
Задача оптимального размещения логистических мощностей давно уже стала классической задачей логистики. В ней требуется найти такое расположение распределительных центров или складов относительно своих поставщиков и потребителей, при котором некая целевая функция, обычно выражающая суммарные логистические затраты, достигает своего минимального значения. Оптимальное месторасположение распределительного центра зависит от многих факторов. Помимо расстояний, объемов перевозимых грузов и транспортных тарифов, на их оптимальное размещение оказывают влияние и такие факторы, как наличие развитой сети подъездных путей (железнодорожных и автомобильных), перспективы и стоимость строительства новых путей сообщения в регионе, целесообразность и затраты на строительство новых распределительных центров или складов в рассматриваемом регионе, экологические и правовые ограничения, налоговые нормы и множество других. И только комплексный учет всех значимых факторов позволяет принять правильное решение об оптимальном размещении распределительного центра в регионе. Математически такая задача соответствует многокритериальной оптимизации при наличии системы ограничений и ее эффективное решение возможно только посредством разработки специализированного программного обеспечения.

Однако прежде чем решать комплексную задачу оптимизации, учитывающую все множество определяющих оптимальное решение факторов, необходимо сначала располагать методом определения оптимального расположения склада, учитывающего такие основные факторы, как расстояния между складом и поставщиками и потребителями, объемы перевозимых грузов, транспортные тарифы и время доставки грузов от поставщиков на склад и со склада потребителям.
Математически задача заключается в определении координат (x, y) склада таких, что логистические издержки, равные сумме произведений расстояний от поставщиков до склада и от склада до всех потребителей, имеющих координаты (xi, yi), на объемы перевозимых грузов Qi (потребность или спрос), были минимальны, т.е.

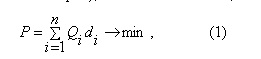
где di – расстояние от склада до i-го потребителя или поставщика, i=1, 2, … n. 
Между тем, до сих пор в существующей литературе по логистике нет полной ясности в том, каким методом необходимо определять координаты склада, чтобы обеспечить минимум целевой функции P и тем самым обеспечить оптимальное расположение склада относительно своих потребителей и поставщиков. 

Несостоятельность метода «центра тяжести» для нахождения оптимального размещения склада
Наиболее распространенным методом определения оптимального месторасположения склада, приводимым практически во всех монографиях, учебниках и учебных пособиях по логистике, является так называемый метод «центра тяжести». Согласно этому методу, координаты размещения склада x и y определяются по формулам:

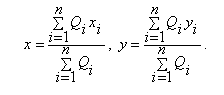
Однако уже на простейших примерах нетрудно показать, что найденные методом центра тяжести координаты (x, y) склада не являются оптимальными, поскольку не доставляют минимума целевой функции (1). 
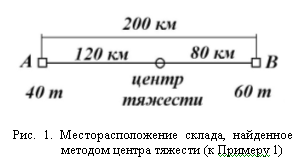
Пример 1. Если два пункта потребления A и B соединены прямой дорогой протяженностью 200 км и в пункт A необходимо ежедневно доставлять 40т продукции, а в пункт B – 60т (рис. 1,а), то по методу центра тяжести склад необходимо разместить между пунктами A и B на расстоянии равном (40•0 + 60•200)/100 = 120 км от пункта A. При таком размещении склада целевая функция будет равна 
P = 40•120 т•км + 60•80 т•км = 9600 т•км.
Между тем, при размещении склада непосредственно в пункте B, целевая функция составит P = 40•200 = 8000 т•км, что на 1600 т•км меньше целевой функции, определенной методом центра тяжести. 
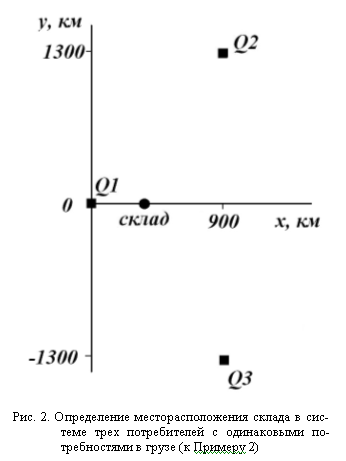
Пример.2. Три пункта потребления расположены в вершинах равнобедренного треугольника. Для простоты примем, что потребности в грузе у всех трех потребителей, одинаковы и равны Q1 = Q2 = Q3 = 300 т. Учитывая симметричность задачи, удобно расположить оси координат так, как показано на рис. 2, тогда координаты (xi, yi), i=1, 2, 3 потребителей будут равны соответственно (0, 0); (900, 1300), (900, –1300). Центр тяжести (или масс) системы расположится вдоль оси x, а по оси ординат, будет иметь координату y = 0. Метод центра тяжести дает для координаты x склада значение

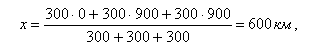
при этом логистические издержки (1) составят

В то же время, если разместить склад на оси x на расстоянии 150 км от начала координат, издержки будут равны

что на 35000 т•км меньше издержек, полученных методом центра тяжести. Отметим значительное расхождение между координатой расположения склада, найденной методом центра тяжести (x = 600 км) и оптимальной координатой его расположения (x = 150 км), при которой значение целевой функции минимально.
Приведенных примеров достаточно, чтобы констатировать, что метод центра тяжести не позволяет определять оптимальное месторасположение склада, при котором целевая функция (1) – сумма произведений расстояний от потребителей до склада на соответствующие объемы спроса потребителей, – была бы минимальной.
Это понятно, потому что в методе центра тяжести ищется не оптимальное место расположения склада, а такое, относительно которого суммарные логистические издержки (Q•d) в любых двух диаметрально противоположных точках области потребления – равны. Другими словами, «центр тяжести» изначально определяется из условия равенства суммарных логистических издержек слева и справа от «центра тяжести» по оси x, и ниже и выше от него – по оси y. Ясно, что такое условие не обеспечивает оптимального размещения склада с точки зрения минимума целевой функции суммарных издержек (1).